The law of regression to the tail
Sir Francis Galton coined the term "regression to the mean" — or "regression towards mediocrity," as he originally called it, sometimes also called "reversion to the mean." It is now a widely used concept in statistics, describing how measurements of a sample mean will tend towards the population mean when done in sufficient numbers, although there may be large variations in individual measurements.
Galton illustrated his principle by the example that parents who are tall tend to have children who grow up to be shorter than their parents, closer to the mean of the population, and vice versa for short parents.
In another example, made famous by Nobel Prize-winner in economics Daniel Kahneman, pilots who performed well on recent flights tended to perform less well on later flights, closer to the mean of performance over many flights. This was not because the pilots' skills had deteriorated, but because their recent good performance was due not to an improvement of skills but to lucky combinations of random events.
There is nothing as practical as a theory that is correct. Regression to the mean has been proven mathematically for many types of statistics and is highly useful in health, insurance, to casinos and in risk management, e.g., for flight safety.
But regression to the mean presupposes that a population mean exists. For some random events of great social consequence this is not the case.
Size-distributions of pandemics, floods, forest fires, earthquakes, wars, terrorist attacks, crimes and IT investments, e.g., have no population mean, or the mean is ill defined due to infinite variance. In other words, mean and/or variance do not exist. Regression to the mean is a meaningless concept for such distributions, whereas what one might call "regression to the tail" is meaningful and consequential.
Regression to the tail applies to any distribution with non-vanishing probability density towards infinity. The frequency of new extremes and how much they exceed previous records is decisive for how fat-tailed a distribution will be, e.g., whether it will have infinite variance and mean. Above a certain frequency and size of extremes, the mean increases with more events measured, with the mean eventually approaching infinity instead of converging. In this case, regression to the mean means regression to infinity, i.e., a nonexistent mean. Deep disasters — earthquakes, tsunamis, pandemics and wars — tend to follow this type of distribution.
I suggest we name this phenomenon — that events return to the tail in sufficient size and frequency for the mean to not converge — "the law of regression to the tail." The law depicts a situation with many extreme events, and no matter how extreme the most extreme event is, there will always be an event even more extreme than this. It is only a matter of time until it appears.
COVID-19 as regression to the tail
Prudent decision makers will not count on luck — or on conventional Gaussian risk management, which is worse than counting on luck, because it gives a false sense of security — when faced with risks that follow the law of regression to the tail. Instead, decision makers will want to do two things: (a) "cut the tail," to reduce risk by mitigation, and (b) practice the precautionary principle, i.e., avoid tail-risk altogether by overcaution.
In any given situation, prudent decision makers and their risk managers must be able to decide whether they face a situation with regression to the mean (mild Gaussian risk) or regression to the tail (extreme fat-tailed risk), and — most importantly — never mistake the former for the latter. This is a difficult task, because a host of cognitive and other biases, including simple wishful thinking, trick us into seeing mild risk when risk is in effect wild.
To illustrate, consider the current COVID-19 pandemic. Pasquale Cirillo and Nassim Nicholas Taleb (2020) have argued that pandemics (measured by number of deaths) seem to follow a Generalized Pareto Distribution. The law of regression to the tail is consequently pertinent, with three important implications.
First, the COVID-19 pandemic was entirely predictable. Indeed, the pandemic was predicted years ago by people as different as Taleb (author of "Incerto"), philanthropist Bill Gates, and numerous epidemiologists who are now, deservedly, having a field day as what-did-I-say prophets, after being ignored for years by government, business and media.
Second, it is clear to anyone who understands regression to the tail what the main mitigating measures should be once a crisis develops, namely: (a) cut the tail (by breaking the chain of transmissions through lockdowns, personal protection equipment, testing, development of vaccines, etc.) and (b) the precautionary principle (rather a lockdown too many than one too few) — rolled out immediately, at speed and at scale, worldwide. The closing of wet markets and changes to the food processing industry will help prevent such a crisis from developing in the first place.
Early mitigation and prevention pay back a thousandfold when facing regression to the tail. Unfortunately, China's leadership delayed mitigation by trying at first to suppress information about the virus. Then, once the data were released, leaders elsewhere — including in the U.S. and the U.K. — were slow to realize they faced extreme risks. Consequently, they were sluggish in making the right decisions. Siloed government also slowed progress.
Third, contingencies must be in place to allow speedy scale-up. When leaders finally understood that COVID-19 was a fat-tailed phenomenon and began to make the proper decisions, it turned out that health services, government and businesses were dismally underprepared, to a degree that things as basic as supplies of face masks, gowns and other protective gear for health workers immediately ran out. The lack of reserves made it impossible to scale effectively and fast — just like a bank without reserves would fail in a crisis.
Due to failure on each of these three points, mitigation in many places was late, slow, and at insufficient scale, that is, the opposite of what is needed when facing regression to the tail, with devastating consequences in terms of lives lost, suffering and wealth destruction.
Two key lessons going forward
To avoid similar failure in the future, leaders and citizens must understand and act in accordance with the law of regression to the tail. In the case of pandemics, there are two lessons to be learnt.
First, everyone needs to be honest about, and keep in mind, that there will be more pandemics in the future, and that one of these will be worse than the COVID-19 pandemic. This uncomfortable fact follows directly from the power-law distribution of pandemics and the associated law of regression to the tail.
Second, once leaders and citizens understand that pandemics involve regression to the tail, they will also understand how to handle the next pandemic: by cutting its tail and employing the precautionary principle immediately, at speed, and at scale, with the necessary contingencies in place.
The two lessons are general. They apply not only to pandemics, but to all phenomena that are subject to the law of regression to the tail, for instance: floods, forest fires, earthquakes, tsunamis, snow avalanches, crime, wars, terrorist attacks, blackouts, bankruptcies and cybercrime, together with less disastrous but financially highly risky ventures like hosting the Olympics, building nuclear power plants, high-speed rail systems, hydroelectric dams, new cities and even something as apparently innocuous as procuring new IT systems, the latter being a serious bug in current worldwide digitization efforts.
Rebuilding the world economy after COVID-19: More tail risk
Rebuilding the world economy after the pandemic will also be subject to the law of regression to the tail. Loss of life will continue to be a main risk in poverty-stricken areas, just as financial fragility and wealth destruction are unfortunately likely to continue for some time.
The massive stimulus spending programs that governments — including the U.S. and China — use to restart depressed economies typically comprise giant construction and investment projects with fat-tailed financial risks, like megaprojects in IT, transportation, energy, water, education, housing, health and defense.
Some projects are more fat-tailed than others, i.e., they are more susceptible to the law of regression to the tail. Data analytics should be used to separate fat-tailed projects from thin-tailed ones, and stick with the latter whenever possible. The data and the analytics to do this exist and are ready for use.
For instance, nuclear power plants and large hydroelectric dams are bespoke, slow to build and fat-tailed for financial risk; whereas wind farms and energy storage are modular, fast and thin-tailed. By choosing wind over nuclear, the risk of regression to the tail will be significantly reduced, and climate goals reached sooner. Elon Musk, CEO of Tesla, and Ørsted, a wind farm company, understand this. Big Energy does not.
Every investment alternative must be assessed in this manner to ensure that stimulus spending becomes a boost instead of a drag on the economy. The latter happens more often than we like to think, when delays and cost overruns become so large that the net benefits of stimulus programs turn negative.
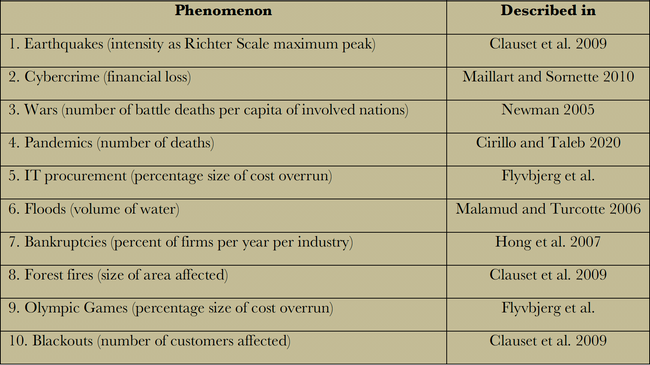
A top 10 of regression to the tail
Table 1 shows a Top-10 list of phenomena that are subject to the law of regression to the tail, ranked by the fatness of tails. All phenomena in the table have infinite variance, i.e., they are highly fat-tailed. We see that the fattest tail — indicating the largest and most frequent regressions to the tail — are found for earthquakes (measured by intensity), which for good reasons are often considered the archetypical case of a power-law distributed deep disaster. Pandemics (measured by number of deaths) are somewhere in the middle, and electricity blackouts (measured by number of customers affected) at the bottom.
Table 1: Top 10 phenomena that are subject to the law of regression to the tail, ranked after fatness of tails. The higher on the list, the fatter the tail, and the larger and more frequent regressions to the tail will be. All phenomena have infinite variance. The table shows phenomena for which data were available.
Four principles of mitigation
For these and the many other phenomena that follow the law of regression to the tail, the implications are clear: Events will always regress to the tail, i.e., to extreme outcomes, and sooner or later there will be an event more extreme than the most extreme to date, often placing lives and wealth at risk. It is similarly clear that four effective mitigation measures exist:
- Cutting the tail;
- Using the precautionary principle;
- Making sure the necessary contingencies are in place; and
- Taking action immediately, at blitz-like speed, and at massive scale.
These are the four basic principles for mitigating risk in the age of regression to the tail.
If we follow these principles proactively, regression to the tail will be mostly manageable. If we don't, tail events will come back to haunt us, over and over, causing unnecessary carnage while we scramble reactively to put in place measures that anyone who understands regression to the tail would agree should have been ready long before we ended up in the tail, as with the COVID-19 pandemic.
Climate change: The über-tail risk
Many have rightly observed that COVID-19 may end up being a mere dress rehearsal for the biggest and most urgent tail risk we face today: climate change. If climate science is right — and there is no reason to think it is not — the law of regression to the tail will be particularly pertinent here. The law says that massive loss of life and wealth will likely follow if climate change is not mitigated now, at speed and at unprecedented scale, with no time to waste in each step involved.
The law of regression to the tail further tells us what the focus for climate mitigation must be: (a) identifying which mitigation measures are particularly scalable at blitz-like speeds and which are not, and (b) accelerating and ramping up measures that are, while ruthlessly scrapping those that are not, because we have no time to waste.
If we do this – i.e., if we truly understand the urgency of the law of regression to the tail for climate change – we have a chance to survive this particular tail risk. If we don't, it will likely mean farewell to the world as we know it, in a mass destruction of lives and wealth, making COVID-19 seem like a picnic in comparison.

Shares